Towards Anything2Vec

June 14, 2015

Like pretty much everyone, I'm obsessed with word embeddings word2vec or GloVe. Although most of machine learning in general is based on turning things into vectors, it got me thinking that we should probably be learning more fundamental representations for objects, rather than hand tuning features. Here is my attempt at turning random things into vectors, starting with graphs.

The key to word embedding algorithms is that there is a boatload of quasi-labelled data since 1) the primary source of words are as part of sentences and 2) the words surrounding a given word are meaningful. The ability to derive meaning from the structure of words is why word embedding models train to predict a word given the context surrounding it (or vice versa). Training is so successful precisely because there is so much free labelled data.

Words are an example of an object where meaning can be derived from structure and crucially, most of the data is structured. But the fun thing is that most objects come as part of some structure, where there is at least some meaning in the structure. For example, people are nodes in social networks with the structure, connections between people, also meaningful. Since this is particularly true of graphs, where the structure is readily apparent, I decided to implement a graph2vec algorithm in Theano based on GloVe. Turns out someone already thought of this, DeepWalk, based on word2vec instead of GloVe but no matter, I'm not in grad school anymore and Theano is fun.

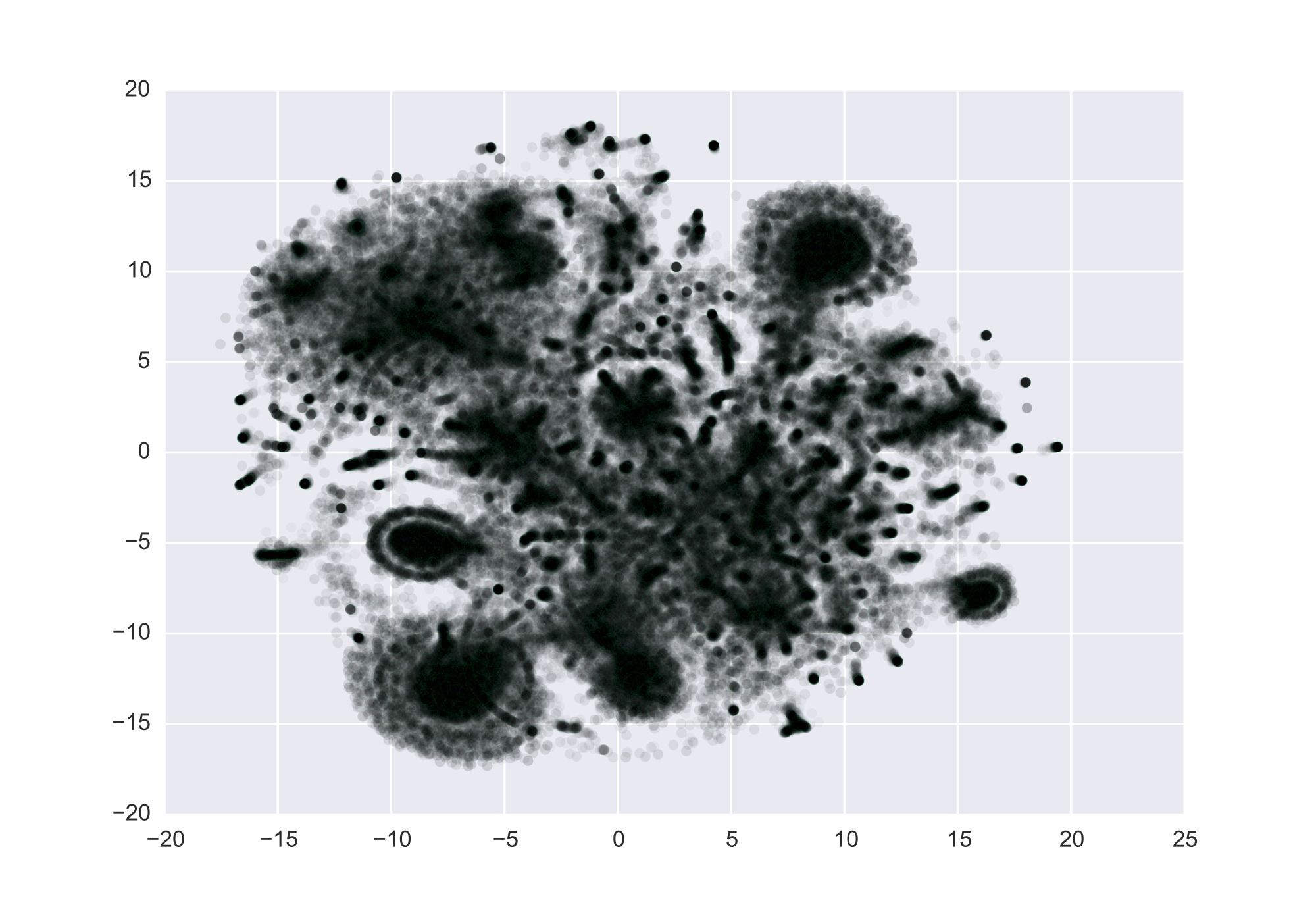
Chart of CPS data — Figure 1: U.S patent vectors in 2D

Above are the (t-SNE'd) vector representations of U.S patents, based on patent citations between 1976-2006 (source: NBER). I treat patent citations as a directed graph, patents as nodes and citations as edges, and train the representations to predict the inverse of the length of the path to a neighbor, capping the length of paths at 2. The loss function is:

$$\mathbb{L} = \sum_{p} \sum_{p' \vert g(p, p') < k} w(g(p, p')) \left( x_p' \hat{x}_{p'} - \frac{1}{g(p, p')} \right)^2 $$

where $ p $ is a node, $g(p, p')$ is the shortest path between two nodes, $w(p, p')$ is a weighting function and $k$ is the max distance of paths included in the estimation.

I don't have any king - man = queen tricks but for what it's worth, the closest patent to PageRank was a patent assigned to Centor Software Corporation, who have a bunch of patents on search and information retrieval (I was hoping for Altavista, which does okay but is no Centor). For those of you that are interested, the code is here.

Intuitively, the algorithm will learn representations such that patents with similar sets of cited or citing patents will be near each other. Note that the clustering itself is not so innovative, since a graph database and suitable queries can do the same thing. What is useful however, are the learned representations, which can be used directly in machine learning models, either in addition to hand tuned features or like in modern NLP, as the features themselves. For example, if you have social network data, learn vectors for each person and train a model of dating. It'd be fun to see if it would learn gender and even sexual preferences.